- ご利用のお客様へ
- ご利用ガイド
- 参考技術情報
- 単位・記号・基本計算式
- 材料の物理的性質、体積・重量の求め方
材料の物理的性質、体積・重量の求め方
金属材料の物理的性質や体積、重量の求め方を掲載しています。
金属材料の物理的性質
| 材質 | 比重 | 熱膨張係数 | 縦弾性係数 | |
| x10-6/℃ | N/mm2 | {kgf/mm2} | ||
| 軟鋼 | 7.85 | 11.7 | 205800 | {21000 } |
| NAK80 | 7.8 | 12.5 | 200900 | {20500 } |
| SKD11 | 7.85 | 11.7 | 205800 | {21000 } |
| SKD61 | 7.75 | 10.8 | 205800 | {21000 } |
| SKH51 | 8.2 | 10.1 | 218540 | {22300 } |
| 超硬 V30 | 14.1 | 6 | 548800 | {56000 } |
| 超硬 V40 | 13.9 | 6 | 529200 | {54000 } |
| 鋳鉄 | 7.3 | 9.2~11.8 | 73500~102900 | {7500~10500 } |
| SUS304 | 8.0 | 17.3 | 193060 | {19700 } |
| SUS440C | 7.78 | 10.2 | 199920 | {20400 } |
| 無酸素銅 C1020 | 8.9 | 17.6 | 114660 | {11700 } |
| 6/4黄銅 C2801 | 8.4 | 20.8 | 100940 | {10300 } |
| ベリリウム銅 C1720 | 8.3 | 17.1 | 127400 | {13000 } |
| アルミニウム A1100 | 2.7 | 23.6 | 67620 | {6900 } |
| ジュラルミン A7075 | 2.8 | 23.6 | 70560 | {7200 } |
| チタン | 4.5 | 8.4 | 103880 | {10600 } |
体積の求め方
| 立体 | 体積V | |
|---|---|---|
| 截頭円柱 |  | \begin{align} V &= \frac{\pi}{4}d^2 h \\ &= \frac{\pi}{4}d^2 \left(\frac{h_1+h_2}{2} \right) \end{align} |
| 角すい | 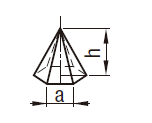 | \[V=\frac{h}{3}A=\frac{h}{6}arn\] \(A\)=底面積 \(r\)=内接円の半径 \(a\)=正多角形の辺の長 \(n\)=正多角形の辺の数 |
| 球冠 | 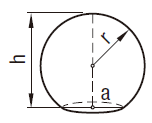 | \begin{align} V &= \frac{\pi h^2}{3}(3r-h) \\ &= \frac{\pi h}{6}(3a^2+h^2)\\ \end{align} \(a\)は半径 |
| 楕円体 | 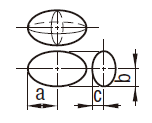 | \begin{equation} V=\frac{4}{3}\pi abc \end{equation} 回転楕円体 (\(b=c\)) のときは \begin{equation} V=\frac{4}{3}\pi ab^2 \end{equation} |
| 楕円環 | 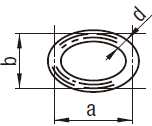 | \[V=\frac{\pi^2}{4}d^2\frac{\sqrt{a^2+b^2}}{2}\] |
| 交叉円柱 | 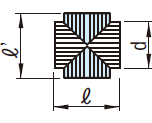 | \[V=\frac{\pi}{4}d^2(\ell+\ell^{\prime}-\frac{d}{3})\] |
| 中空円柱(管) | 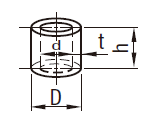 | \begin{align} V &= \frac{\pi}{4}h(D^2-d^2) \\ &= \pi th(D-t) \\ &= \pi th(d+t) \end{align} |
| 截頭角すい | 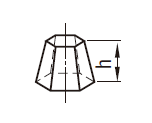 | \[V=\frac{h}{3}(A+a+\sqrt{Aa})\] \(A,a\)=両端面の面積 |
| 球分 |  | \begin{align} V &= \frac{2}{3}\pi r^2 h \\ &= 2.0944r^2 h \end{align} |
| 円環 | 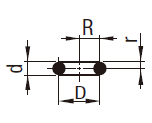 | \begin{align} V &= 2\pi^2Rr^2 \\ &= 19.739Rr^2 \\ &= \frac{\pi^2}{4}Dd^2 \\ &= 2.4674Dd^2 \end{align} |
| 円すい | 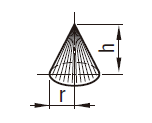 | \begin{align} V &= \frac{\pi}{3}r^2 h \\ &= 1.0472r^2 h \end{align} |
| 球 | 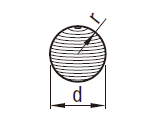 | \begin{align} V &= \frac{4}{3}\pi r^3=4.1888r^3 \\ &= \frac{\pi}{6}d^3=0.5236d^3 \end{align} |
| 球帯 | 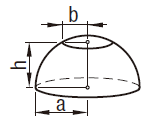 | \[V=\frac{\pi h}{6}(3a^2+3b^2+h^2)\] |
| 樽形 | 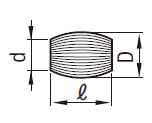 | 円周が円弧に等しい彎曲をなすときは \begin{equation} V=\frac{\pi \ell}{12}(2D^2+d^2) \end{equation} 周囲が放物線に等しい彎曲をなすときは \begin{equation} V=0.209\ell(2D^2Dd+1/4d^2) \end{equation} |
重量の求め方
重量W[g]=体積[cm3]×比重

[例]材質:軟鋼
\begin{align}
D &= \phi16、L=50mm の重量は\\
W &= \frac{\pi}{4}D^2\times L\times 比重 \\
&= \frac{\pi}{4}\times 1.6^2 \times 5 \times 7.85 \\
&≒ 79[g]
\end{align}
| 最新更新年月日: 2023年6月23日 ※ 本稿は21年6月時点の最新情報を掲載しています。 |